지난번 온라인 알고리즘의 포스팅에서 간략하게 온라인 알고리즘을 설명했다면, 이번 포스팅에서는 Minimization 문제인 maskespan problem의 솔루션 중의 하나인 Graham’s greedy makespan algorithm를 분석해보도록 하겠습니다.
우선 들어가기에 앞서 determinisic online 알고리즘 문제를 정의하는 하나의 템플릿을 소개하겠습니다.
request-answer game은 determinisic online 알고리즘을 정형화하는 일종의 템플릿입니다. 정의는 간단합니다.
온라인 알고리즘은 연속된 요청(request)를 σ = σ(1), . . . , σ(m) 받습니다.
이 요청들은 순서가 있으며, σ(t)의 요청을 받았을 때, σ(t ′ ) ,t ′ > t를 알지 못한 상황에서, 전체 요청에 대해서 최소화하는 혹은 최대화하는 것이 목표입니다.
Minimization Problem: makespan
이번에는 makespan 문제의 competitive ratio를 정리해보도록 하겠습니다. 우선 makespan 문제는 다음과 같이 정의할 수 있습니다.
$ L = {J_1, J_2, ..., J_n}$ 만큼의 일이 주어지고 각각의 일들은 프로세싱 타임 $p_i$로 표현된다. 그리고 일들을 처리하기 위한 머신들의 개수를 $m$ 이라 할때, $n$개의 일들을 $m$개의 machine들에 배치하여 프로세싱 타임이 최소가 되게 하는 $r: {1,2,...n}$ → ${1,2,...,m}$ 을 구하시오.
이 문제를 풀기위해서는 다양한 방식이 있겠지만 우선 가장 기본적인 그리디 알고리즘으로 분석을 해보도록 하겠습니다. 이 문제에서 그리디한 접근방식은 순차적으로 일이 들어올 때마다 현재 가장 일이 적은 머신에 일을 할당해주는 알고리즘입니다. 그렇다면 이 알고리즘은 얼마나 좋은 알고리즘일까요? 우리는 우선 다음과 같이 정리할 수 있습니다.
우선 알고리즘 G는 모든 인풋에 대하여 임의의 c-근사를 가지고 있습니다.
$$Cost(G(I)) \le c * Cost(OPT(I))$$
여기서 OPT는 모든 인풋을 통해 얻을 수 있는 오프라인 알고리즘의 optimal 값이고 Cost의 의미는 알고리즘을 통해서 얻을 수 있는 솔루션의 비용입니다.
우리는 물론 optimal 알고리즘보다 더 잘할 수 없으므로 c 는 1보다 크거나 같을 것입니다.
일반적으로, inapproximation bounds를 증명하는 방법으로는 몇가지가 있는데,
- charging argument
- promising solution
- observing properties of the optimal solution
3번째 방법으로 증명을 하도록 하겠습니다.
proof. 일반적인 인풋을 가정할 때, 우리는 optimal 값은 적어도 가장 긴 프로세스보다 오래 걸린다고 할 수 있습니다.
$$OPT(I) \ge \max_{{j}} p_j$$
그리고 우리는 전체 프로세스의 합을 머신들의 개수로 나누는 거보다 오래 걸린다고 나타낼 수 있습니다.
$$OPT(I) \ge (\sum_{j}p_j)/m$$
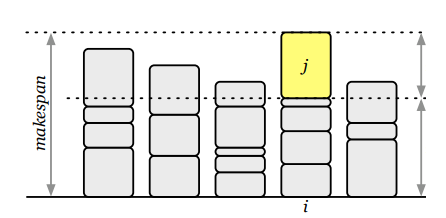
이제 그리디 알고리즘에 대해서 생각해봅시다. $C_max$를 최종 비용이라고 할 때, 이 의미는 일을 가장 늦게 끝내는 머신의 비용일 것입니다. 그리고 $p_k$를 이 머신의 마지막 프로세스라고 할 때, 우리는 $p_k$가 이 문제를 결정한다고 말할 수 있습니다.
$p_k$가 스케줄링될 때, 스케줄링되는 머신은 가장 적은 일을 가지고 있는 상태입니다.
그렇다면 $C_{lowest-kth} = C_{max} - p_k$라고 할 수 있습니다.
그리고 알고리즘의 정의에 따라서 $C_{lowest-kth} \le (\sum_{k\ne j}p_j)/m$ 임을 알 수 있습니다.
$$C_{max} = C_{lowest-kth} + p_k$$
$$\le (\sum_{k\ne j}p_j)/m+p_k$$
그리고 $OPT(I) \ge (\sum_{k\ne j}p_j)/m + p_k/m$ 을 생각한다면, $$C_{max} \le (\sum_{k\ne j}p_j)/m+p_k$$
$$= (\sum_{k\ne j}p_j)/m+p_k/m+ p_k$$
$$\le OPT -p_k/m +p_k$$
$$= OPT + p_k(1-1/m)$$
$$\le OPT - OPT(1-1/m)$$
$$= (2-1/m)OPT$$
이로써, $G(I) \le (2-1/m)OPT(I)$의 bound가 성립합니다. 하지만 $m \ge 4$일 때, 이 그리디 알고리즘의 bound보다 더 효율적인 알고리즘들이 존재합니다. 현재 알려진 가장 좋은 알고리즘은 모든 m에 대한 upper bound는 1.901, lower bound는 충분히 m이 클 경우에 1.88이라고 합니다.
Longest processing time 알고리즘(이하 LPT 알고리즘)은 그리디 알고리즘의 일종으로 작업들의 processing time이 정렬되어 있어야 한다는 점에서 완전한 온라인 알고리즘은 아니지만 maskspan 문제에서 괜찮은 approximation-ratio를 보장하는 알고리즘입니다. 알고리즘은 간단합니다.
n개의 작업들 $ {p_1, p_2, p_3, ...,p_n} $이 있다고 할 때
- 작업들을 processing time에 따른 내림차순으로 정렬합니다.
- 그리디 알고리즘과 마찬가지로 가장 적게 할당받은 머신에 작업을 할당합니다.
이 알고리즘은 $\cfrac{4}{3} - \cfrac{1}{3m}$의 approximation ratio를 가지고 있습니다.
한번 증명을 정리해보도록 하겠습니다.
우선 다음 lemma를 정의해야 합니다.
$$ \text{if } p_{min} > OPT/3 \text{, then } C_{max} = OPT $$
$p_{min} > OPT/3$를 가정한다면 $OPT < 3p_{min}$ 가 성립합니다.
이는 OPT 알고리즘은 한 머신에서 3개 이상의 작업은 못한다는 것을 의미합니다.
만약에 LPT 알고리즘이 3개의 작업을 한 머신에 할당한다면, j를 한 머신에 할당되는 3번째 작업이라고 합시다. $n\le 2m$이라면, OPT 알고리즘이 아닌 LPT 알고리즘일 경우에는 k번째 작업을 하나 할당받은 머신이 존재합니다. 그리고 LPT 알고리즘에 의하여 task를 가장 적게 할당받은 머신이 할당한다면, 이것은 k가 다른 2개의 task를 받은 머신보다 긴 시간이라는 것을 의미합니다. $p_k \ge 2p_{min}$가 성립하는 것을 알 수 있습니다.
결국 OPT 알고리즘에서 다른 태스크와 함께 할당된다면, $p_k + p_{min} > OPT$가 되기 때문에 모순이 생깁니다.
그리고 $p_{min} \le OPT/3$이고, $p_{min} = p_{n}$이라 한다면 우리는 다음과 같은 bound를 얻을 수 있습니다.
$$C_{max} \le OPT + (1-1/m)p_{n} \le \cfrac{4}{3} - \cfrac{1}{3m} OPT$$
물론 이보다 더 좋은 PTAS라는 알고리즘이 있습니다. 이 알고리즘은 다음에 한번 다뤄보도록 하겠습니다.
다음 포스팅에서는 maximization 문제인 Time-series search에 대해서 분석을 해보도록 하겠습니다.
'알고리즘 > online algorithm' 카테고리의 다른 글
| Online 알고리즘 (5) - Randomized Online Algorithms (MBG 문제) (0) | 2020.05.02 |
|---|---|
| Online 알고리즘 (4) - Randomized Online Algorithms (1) (0) | 2020.04.28 |
| Online 알고리즘 (3) - Deterministic Online Algorithms (2) (0) | 2020.04.19 |
| Online 알고리즘 (1) - Online Algorithm (0) | 2020.04.05 |



